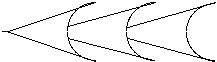The essence of the principle of asymmetric transitions is that the probability of transition from state A to state B is in general different from the transition probability of B to A. This leads to evolution with a preferred direction: A -> B is more likely than B -> A. It is not necessary to imagine complex living systems or esoteric far-from-equilibrium thermodynamic set-ups to illustrate this idea. The most obvious illustration is the behavior of heavy objects that are subject to gravity and friction. If you drop a stone or ball down a slope it will normally move downwards until it finds a stable position, and not move upwards anymore. (in the unrealistic case where there is no friction, the ball will bounce back, and continue to go up and down like a jojo, until the end of time).
One might object that this is not a good illustration of the process of evolution since there is an external force, gravity, which pulls the system in a determined direction, unlike most other evolutionary systems which undergo blind variation without any sense of direction. However, it is easy to devise systems that move in a specific direction because of asymmetric transitions, independently of, or even in spite of, forces pushing them in a different direction.
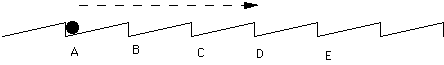
Imagine the following set-up (see fig.), where a ball is positioned on a surface that looks like a slightly skewed horizontal staircase. The vertical wall of the stair makes it impossible for the ball to move to the left. However, the ball needs just a small impulse to move over the gently inclining slope on the right and reach the next stair (B). In that next state, again moving back to the left is precluded, while continuing movement to the right (C) is relatively easy. Thus we have a system where P(A->B) >> P(B->A). We can imagine that if the whole set-up is gently shaken (in random directions, i.e. blind variation), the ball will move more and more to the right and never come back.
We could even imagine that the set-up as a whole is not horizontal but slightly inclined so that position B is elevated with respect to A, and C with respect to B, etc. In that case, the random moves would make the marble effectively move upwards, against the force of gravity. We could also imagine a "staircase" forming a loop so that position Z is identical to position A (as in a famous Escher drawing where figures are climbing up a staircase that turns back into itself). In that case, the marble will just continuously cycle along the staircase, like in a 1 dimensional attractor. With a two dimensional design, much more complex figures are possible, including fractal attractors.
An alternative set-up is one where it is not the environment (the staircase) that has an asymmetrical effect, but the system (marble) itself. For example, some seeds are shaped such that they can easily enter a tissue (or animal fur), but it is almost impossible to pull them back (see Fig.). The only way to get rid of them is by pulling them forward in the direction they originally entered.