The main innovation of thermodynamics is the idea that different causes lead to the same effect, the state with maximum entropy. This equilibrium state to which all other states converge can be seen as an attractor: it is as if it attracts different possible states of the system, so that all trajectories come together in the same point. For example, if you let a pendulum move freely, after a few oscillations it will slow down and come to rest in its lowest position, whatever the position it started from. The initial differences in the starting positions (causes) are gradually reduced until they completely disappear.

Fig. 3: a point attractor: the arrows represent trajectories starting from different points but all converging in the same equilibrium state
Let us now make the system non-linear. This means that we will add a force which amplifies differences. The combination of the two influences, one dampening differences, one amplifying them, can produce the most complicated behaviors. The simplest one is just a regular oscillation, which never stops, like the pendulum of a clock which is powered by a spring. This pattern of movement is again an attractor, since different initial positions of the pendulum will all converge on the same periodic trajectory. But such an attractor no longer consists of a single point, but of a closed, one-dimensional line of points. This is called a limit cycle, since it represents the closed trajectory in which the system will settle in the limit. (It is ironic that the traditional mechanical clock, whose regular movement became a paradigm for classical mechanics, in fact achieves this regularity through the balance of two opposing, non-classical forces.)
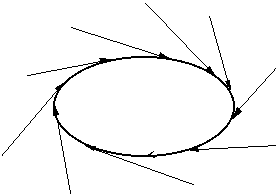
Figure: a 1 -dimensional attractor or limit cycle. The arrows correspond to trajectories starting outside the attractor, but ending up in a continuing cycle along the attractor.
When the non-linearity of the system becomes more important, more complicated attractors may appear. The final trajectory in which the system settles may have a very irregular shape, without any apparent periodicity. Yet, this eventual trajectory is still an attractor, because neighbouring trajectories are "sucked" into it, losing their freedom to get out again. In general, an attractor is a region in the space of possible states which the system can enter but not leave. In that sense, an attractor is like a "black hole" in space, constantly sucking in material, but never letting anything go. That region can have different dimensions, of which the zero-dimensional point attractor, and the one-dimensional limit cycle are just the simplest cases. Attractors with non-integer, fractal dimensions are called strange attractors. Trajectories moving inside a strange attractor are totally chaotic.
Another characteristic of highly non-linear systems is that they have in general several attractors. A simple thermodynamical system, on the other hand, has only one attractor, the maximum entropy state. When there is more than one attractor, the main question is in which of those attractors the system will end up. Imagine that each attractor corresponds to a lake or sea, and that the trajectories leading into an attractor correspond to the rivers and streams flowing into those lakes. Depending on where it falls, rainwater will follow either one river or another, ending up in either one lake or another. The complete area drained by a river is called its basin. Similarly, each attractor has a basin, which is the surrounding region in state space such that all trajectories starting in that region end up in the attractor. The basins belonging to different attractors are separated by a narrow boundary, which can have a very irregular shape. For initial positions close to the boundary, it is very difficult to determine to which attractor they lead. Small fluctuations can push the system either into the one or into the other basin, and therefore either into the one or into the other attractor. (see Figure 5). The appearance of such a border separating two attractors is called a bifurcation. Close to the border, the system behaves chaotically, inside the basin it moves predictably towards the attractor.
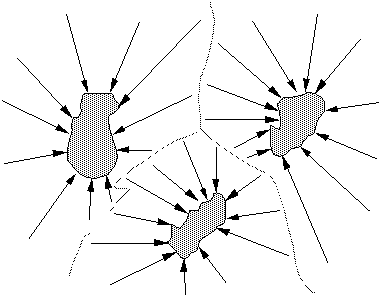
Fig. 5: three attractors with some of the trajectories leading into them. Their respective basins are separated by a dotted line.
When a dynamical system is put under stress, for example by increasing the energy or flow through it, the number of attractors tends to increase. One way to understand this is by noting that more energy allows more amplification of small differences, and therefore more varied types of behavior. Suppose you start with one attractor. When you increase the stress, you get a bifurcation: the attractor splits in two. The system now has two stable patterns of behavior. For example, imagine that you let water run through a tap. When the water runs very slowly, it comes out in regular, periodically falling drops. When you open the tap a little bit more, it may happen that there are two patterns of running: either big drops succeeding each other quickly, or a thin, continuous stream. Sometimes you have the one pattern, sometimes a slight fluctuation in the pressure makes the water switch to the other pattern. When the stress is increased further, more bifurcations take place, and the attractors split up further. First, you have 4 possible regimes, then 8, then 16, then 32, and so on, ever more quickly. At a certain point, the number of attractors becomes infinite and the system is erratically jumping from the one to the other all the time. This is true chaos. The behavior of the system has become totally unpredictable. Coming back to the water tap, this is what happens when the tap is opened fully and the water is running out turbulently, in one big, irregular waterfall, with droplets spraying in all directions.

