Although acceleration and complexity have made most concrete developments
impossible to predict, large scale, statistical factors, such
as wealth, life expectancy, intelligence, productivity, speed of information
transmission and speed of information processing, increase in a surprisingly
regular way. This makes it possible to extrapolate their development into the
future. Most of these growth processes are exponential, characterized by a
constant doubling period, or a constant increase in percentage per year. This
means that the underlying growth mechanism is stable, producing a fixed number
of new items for a given number of existing ones.
However, some processes grow even more quickly. For example, population growth
in percentage per year is much larger now than it was a century ago. This is
because medical progress has augmented the gap between the percentage of births
and the percentage of deaths per year. If the growth of the world population
over the past millenia is plotted out, the pattern appears to be
hyperbolic rather than exponential. Hyperbolic growth is characterized
by the fact that the inverse of the increasing variable (e.g. 1 divided by the
total population) evolves according to a straight line that slopes downward. When the line reaches zero, this means that the variable (world
population in this case) would become equal to 1 divided by zero, which means
infinity. This is essentially different from an exponential growth process,
which can never reach infinity in a finite time.
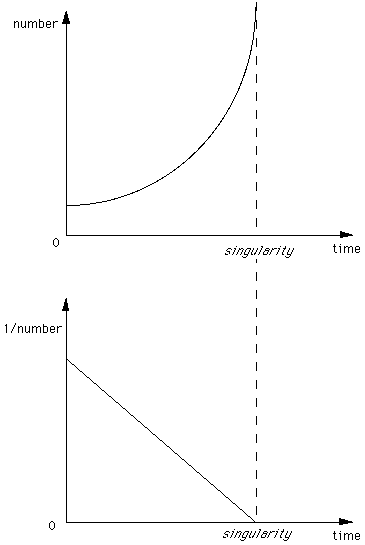
Fig. 1: a hyperbolic growth process, where the growing number becomes infinite
in the singular point, while its inverse (1 divided by the number) becomes
zero.
If the line describing the inverse of world population until recently is
extended into the future, we see that it reaches zero around the year 2035. Of
course, such an extrapolation is not realistic. It is clear that world
population can never become infinite. In fact, population growth is slowing
down at this moment. However, that slowdown itself is a revolutionary event,
which breaks a trend that has persisted over all of human history.
In mathematics, the point where the value of an otherwise finite and
continuous function becomes infinite is called a "singularity". Since
traditional mathematical operations, like differentiation, integration and
extrapolation, are based on continuity, they cannot be applied to this singular
point. If you ask a computer to calculate the value of one divided by zero it
will respond with an error message. A singularity can be defined as the point
where mathematical modelling breaks down. The inside of a "black hole" is an
example of a singularity in the geometry of space. No scientific theory can say
anything about what happens beyond its boundary. We can only postulate that
different laws will apply inside, but these laws remain forever out of sight.
Similarly, the Big Bang, the beginning of the universe, is a singularity in
time, and no amount of extrapolation can describe what happened before this
singular event.
The mathematician and science fiction writer  Vernor Vinge has
Vernor Vinge has  proposed that
technological innovation is racing towards a singularity. Scientific discovery appears as an exponentially growing process with a
doubling period of about 15 years. However, the doubling period is
diminishing because of increasingly efficient communication and processing of
the newly derived knowledge. The rate of growth is itself growing. This makes
the process super-exponential, and possibly hyperbolic. Vinge would argue that
at some point in the near future the doubling period would reach zero, which
means that an infinite amount of knowledge would be generated in a finite time.
At that point, every extrapolation that we could make based on our present
understanding would become meaningless. The world will have entered a new
stage, where wholly different rules apply. Whatever remains of humanity as we
know it will have changed beyond recognition.
proposed that
technological innovation is racing towards a singularity. Scientific discovery appears as an exponentially growing process with a
doubling period of about 15 years. However, the doubling period is
diminishing because of increasingly efficient communication and processing of
the newly derived knowledge. The rate of growth is itself growing. This makes
the process super-exponential, and possibly hyperbolic. Vinge would argue that
at some point in the near future the doubling period would reach zero, which
means that an infinite amount of knowledge would be generated in a finite time.
At that point, every extrapolation that we could make based on our present
understanding would become meaningless. The world will have entered a new
stage, where wholly different rules apply. Whatever remains of humanity as we
know it will have changed beyond recognition.
Some data supporting this conjecture can be found in a chart provided by Peter
Peeters, in which the time elapsed between a dozen fundamental discoveries and
their practical application is plotted against the year in which the invention
was applied. The graph shows a downward sloping line, which reaches zero in the
year 2000. These are just a few data points, and the implication that
inventions will be applied virtually instantaneously after 2000 does not yet
mean that scientific progress will be infinite. Vinge himself would situate the
date of the singularity between 2010 and 2040. His reasoning is based on the
accelerating growth of computer-aided intelligence. Rather than considering the
IQ of an isolated individual, he would look at the team formed by a person and
computer. According to Vinge, a PhD armed with an advanced workstation should
already be able to solve all IQ tests ever devised. Since computing power
undergoes a rapid exponential growth, we will soon reach the stage where the
team (or perhaps even the computer on its own) would reach superhuman
intelligence. Vinge defines this as the ability to create even greater
intelligence than oneself. That is the point at which our understanding, which
is based on the experience of our own intelligence, must break down.
A related reasoning was proposed by Jacques Vallée. Extrapolating from
the phenomenal growth of computer networks and their power to transmit
information, he noted that at some point all existing information would become
available instantaneously everywhere. This is the "information singularity".
These models should not be taken too literally. They are metaphors, proposed
to stimulate reflection. It does not make much sense to debate whether "the
Singularity", if such a thing exists, will take place in 2029 or in 2035.
Depending on the variable you consider most important, and the range over which
you collect data points, you may find one date in which infinity is reached, or
another, or none at all. Even if nothing as radical as a "New Age" could be
predicted, the zero point method is certainly useful to attract the attention
to possible crisis points, where the dynamics of change itself are altered.
Peeters has used this method with some success to "predict" historical crises,
such as the First World War and the 1930 and 1974 economic recessions. (The
Second World War, strangely enough, did not seem to fit the model...).
The point to remember, however, is that abstract, non-material variables, such
as intelligence, information, or innovation, aren't subjected to the same
"limits to growth" which characterize the exhaustion of finite resources. Such
variables could conceivably reach values which for all practical purposes may
be called "infinite". Several parallel trends show a hyperbolic type of
acceleration which seems to reach its asymptote (the point of infinite speed)
somewhere in the first half of the 21st century. This does not mean that actual
infinity will be reached, only that a fundamental transition is likely to take
place. This will start a wholly new mode of development, governed by laws which
we cannot as yet guess.
References:

