ABSTRACT. It is argued that in order to tackle a complex problem domain the first thing to do is to construct a well-structured problem formulation, i.e. a "representation". Representations are analysed as systems of distinctions, hierarchically organized towards securing the survival of an agent with respect to his situation. A preliminary variation-selection model is proposed for the generation of new distinctions. A research project for building a general model of representation construction is outlined, combining theoretical, computational and empirical-psychological approaches.
1. Introduction
Until now the theory of problem-solving (e.g. Newell and Simon, 1972) has mainly emphasized the search of solutions within a problem space. From this viewpoint, problem-solving capability (i.e. intelligence) should be seen as the possession of adequate heuristics, which allow to make the search more efficient. This view presupposes that the search space is explicit and well-structured, i.e. that at each decision point there is a well-defined set of operators (or problem states to be generated) from which the most promising can be chosen according to some heuristic rule.
This approach is typically applied in "game" situations (e.g. chess) and "toy" problems (e.g. the tower of Hanoi problem), where the possible "moves" are fixed by predetermined rules. As we all know, games and toys are primarily used by children (and adults) to learn about the world by playing, i.e. by performing simulations of actions so that the result of these actions can be explored without being confronted with the complexities and dangers of the real world. In this sense we have learned a lot about problem-solving and about intelligence by constructing computer models of how to play games or how to manipulate toys.
However, this does not mean that we are able to build models of how to cope with the real world. Recently, the awareness has been growing in AI that, in order to get insight into practical intelligence, we need to build autonomous agents (e.g. robots) capable of directly interacting with a real environment. However, in order to experiment efficiently with such systems we should simultaneously develop a theory of problem-solving in complex, ill-structured environments. The present paper proposes the outline of a research project, aimed at the construction of such a theory.
First, we should attempt to define an "ill-structured problem environment". It can be characterized, first, by the presence of a "problem", i.e. a situation which is to be changed in some way; second, by the absence of the structure needed for efficient search : well-defined goal(s), problem-states, operators, constraints, heuristic criteria ... In a more radical formulation : when confronted with such a problem, we know that something is to be done, we do not want the situation to evolve on its own, but we do not know what to change, how to change it, or what the result of the change should be like.
Some examples of ill-structured problems may show the practical applicability of the theory we are looking for. The management of a large socio-economic system (e.g. a firm, an organization or a state) is clearly a very complex problem (cfr. Dörner & Reither, 1978; Dörner et al., 1983) : it is in general not at all clear which goals are to be pursued, which means are available, or which information is relevant. The availability of communication and information technology will in general only increase the complexity of decision-making. Indeed, existing computer systems are only capable of solving well-structured problems. In this way they will merely increase the available information and hence the possibilities for choice, without reducing the ill-structuredness of the situation. Another example is research : the development of scientific theories is clearly an ill-structured problem domain. The discovery of new concepts or models is basically a process of building simple structures out of the available data, which are often inconsistent, ambiguous, vague and changeful.
Clearly, the first thing to be done in order to solve an ill-structured problem is to formulate it in a well-structured way, i.e. to describe explicitly the initial situation which is to be changed, the goal which is to be achieved, the problem-space which is to explored, the operators which are to be used, ... Such a well-structured formulation is traditionally called a representation of the problem (cfr. Amarel, 1967; Burghgraeve, 1976; Korf, 1980; Heylighen, 1986). A representation of how to build such representations may then be called a metarepresentation (Heylighen, 1987a,b). Once we know how to construct (and transform) representations of ill-structured problem domains, we can simply apply the existing knowledge about search through problem spaces in order to be able to solve all types of problems. We will now propose a conceptual framework for the analysis of representations.
2. Representations as Distinction Systems.
In order to begin our study, we must analyse the object of the study : representation. A representation can always be considered as a system, i.e. an organized, goal-directed whole of interrelated elements. The goal or function of a representation is to structure the field of experience of the intelligent agent using the representation, in such a way that the agent can search efficiently for solutions when confronted with a problematic situation, which is to be changed.The second question to be asked then is : what are its elements ? The elements we are looking for are primitive structurations of the problem environment as experienced by the agent.
The simplest form or structure we can imagine is a distinction (Spencer-Brown, 1969). A distinction can be defined as the process (or its result) of discriminating between a class of phenomena and the complement of that class (i.e. all the phenomena which do not fit into the class). As such a distinction structures the universe of all experienced phenomena in two parts. Such a part which is distinguished from its complement or background will hereafter be called an indication (Spencer-Brown, 1969). If more than one distinction is applied the structure becomes more complex, and the number of potential indications increases, depending on the number of distinctions and the way they are interrelated.
In contrast to Spencer-Brown (1969), we will not assume any general axioms for distinctions. In particular we will not assume that the complement of the complement a' of an indication a is again the same indication (law of double negation) : (a')' = a . This means that we do not suppose distinctions to be symmetric : the complement or negation a' of an indication a has not necessarily the same status as a. However, if this symmetry property is assumed, together with a related axiom about conjunctions (or disjunctions) of distinctions (the law of idempotence, cfr. Heylighen, 1987a), it can be shown that a set of distinctions gets a Boolean algebra structure, isomorphic to the algebra of classes in set theory or to the algebra of propositions in logic (Spencer-Brown, 1969).
How do distinctions determine problem-solving efficiency ? Clearly, to formulate a problem you need to make a minimum number of distinctions. At least you should be able to distinguish the situation to be changed from the situation corresponding to a satisfying problem-solution. Furthermore, in order to be able to search for a solution you should distinguish different problem-states, which can be reached by distinct operators. The more general you want your representation to be, i.e. the more potential problems you want to be able to solve, the more distinctions you must make.
However, more distinctions means more states, more operators, more decision points, hence more search to be carried out. Clearly, in order to minimize search you must minimize the number of distinctions. This means that for a computationally tractable representation of a real problem domain most phenomena must remain "indistinguishable" (cfr. Hobbs, 1985). In the terminology of (Heylighen, 1987a) : different phenomena are "assimilated" to the same class, which is "distinguished" from other classes.
Assimilation and distinction necessarily go together : the number of potentially distinguishable phenomena in the universe can be considered to be infinite, the number of actual distinctions used for solving a problem in the real world must be finite. Which finite set of distinctions is selected from this infinite set will depend upon the problem domain. The problem of problem-formulation could hence provisionally be formulated as : how to determine the optimal (i.e. minimal, yet large enough to cover all relevant solution paths) set of distinctions for a particular problem domain ?
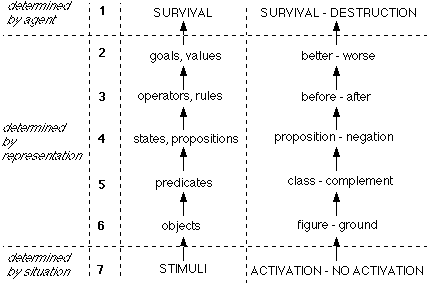
However, a representation is not just a set of distinctions, it is a system. This means that we must first look for the properties of and relations between distinctions, in order to understand how they are organized towards the fulfillment of their function. The structural units of a representation can be described in a hierarchy of levels, ordered from the more "subjective", agent-determined structures, to the more "objective", situation-determined structures (see fig. 1) :
1) a problem is determined first by the autonomous agent, whose ultimate aim is survival; 2) in order to survive the agent must specify more concrete goals or values, which represent classes of situations for which the long-term survival is more probable, and which can be reached by a sequence of actions (cfr. Heylighen, 1988); 3) to attain these goals the system must dispose of a set of operators (also called "(production) rules"), representing possible actions changing the situation; 4) the operators have arguments, which may be called problem-states, and which represent distinguished situations; 5) the states can be analysed as compound logical propositions, consisting of primitive propositions formed according to the Predicate (object) scheme; a predicate may be conceived as a class of phenomena ; 6) an object to which this predicate is attributed corresponds then to an instantiation of that class; 7) finally, the objects and predicates perceived by the agent depend upon the physical stimuli received from the external (or internal) situation of the agent, i.e. by its environment.
Each of these units can be interpreted as a particular type of distinction : 1) the distinction between survival (i.e. maintenance of the identity or self-environment boundary, cfr. Heylighen, 1988) and destruction of the agent; 2) the distinction between "better" situations and "worse" situations. In the General Problem Solver (GPS; Newell & Simon, 1972) these distinctions are called "differences" between goal and non-goal states. The number of such "differences" can then be used as a basic evaluation criterion for states, allowing "hill-climbing" search heuristics; 3) the distinction between the situation before and after the operator has been applied. Clearly, if these situations cannot be distinguished, the operator is meaningless. In GPS these "distinctions" are coupled to the previous ones by a matrix, connecting a list of operators to a list of differences by specifying whether a particular operators is able to reduce a particular difference between the initial state and the state to be attained; 4) propositions describing potential situations form a Boolean algebra which can be interpreted as an algebra of distinctions (Spencer-Brown, 1969). The basic distinction here is that between a proposition and its negation; 5) as we already pointed out, a predicate corresponds to a class, and a class is the result of a distinction between phenomena; 6) an object on the other hand, arises when a stable "form" or "system" is distinguished from its "background" or "environment"; 7) sensory stimuli, finally, are the result of a differential excitation of elmentary receptors (e.g. nerve cells), creating a distinction between "activated" and "non-activated" receptors.

Figure 1 : hierarchy of representation levels and their corresponding distinction levels
3. The Representation of Change.
The simplest way to represent the changes which are to be brought about in order to solve a problem is by keeping all distinctions invariant, and varying only the indications. An indication should be conceived as that part (of all the parts of the universe of experience which are distinguished) that is "indicated", "activated" or "actualized". For example, an intelligent agent can conceive a large number (possibly infinite) of situations, internally represented as "problem states", but at a specific instant in time only one of these situations will be "actual". All the other ones are "potential", they are not yet indicated. An evolution in time, i.e. a sequence of actual situations, will then be represented as a sequence of indications, actualizing one state and then moving on to the next one (Heylighen, 1987a).
During such an evolution only "states" change, all "structures" are conserved. This means that the set of objects, the set of predicates, the state space, the set of operators, the goals, values or heuristics, ..., all remain invariant. A representation functioning according to this scheme may be called classical (Heylighen, 1987a,b). A prototypical example of such a representation is the physical theory of classical mechanics. It is characterized by properties such as determinism, rationality, reversibility, absoluteness of space and time, causality, sequentiality, ... On the level (4) of states, the requirement of distinction conservation signifies that an allowed operator will necessarily map distinct states ("causes") onto distinct states ("effects"), and "equal" states (i.e. states which are not distinguished, which are assimilated) onto "equal" states.
This requirement is clearly not satisfied by the paradigm of search, used for describing heuristic problem-solving. Indeed, it is assumed that in general there is no determined function or algorithm, leading deterministically from the initial state to the goal state. Distinct states have to be explored starting from the same initial state, and distinct initial states can lead to the same goal state. In this sense search representations are similar to the physical representations used in thermodynamics, where state trajectories with distinct starting points may come together (equifinality), or where a trajectory starting from the same initial state can branch, leading to distinct end points (bifurcation)(cfr. Heylighen,1987a).
The evolution of states in the search representation can be summarized by the generate-and-test principle : distinct states are generated from an initial state ; the one (or more) states which are evaluated positively after a test, are retained and used as starting points for a subsequent exploration step. This principle is equivalent to the principles of trial-and-error and variation-and-selection. In each case there is a first phase of variation, i.e. the generation of a variety of new, distinct states ("trials"), followed by a second phase of selective retention, during which all states that are evaluated negatively ("errors") are eliminated. Such a principle could be viewed as a general description of processes in which certain distinctions are destroyed (because distinct initial states can generate the same variations) while other distinctions are generated (because the same initial state can generate distinct, selectively retained variations).
However, although a search representation is non-classical (i.e. non-distinction- conserving) at the level of states, it is still classical at all other levels : during a heuristic search process all objects, predicates, operators, heuristics, and goals, determining the representation structure, are kept invariant. Yet there exist representations which are non-classical at those other levels. For example, the theory of quantum mechanics is characterized by the non-conservation of distinctions at the levels of predicates (Heylighen, 1987a), whereas relativistic quantum field theories describe the non-conservation of object distinctions (annihilation and creation of elementary particles).
The representation of all possible problem-formulation processes we are looking for, however, would be characterized by the possibility of creating or eliminating distinctions at all levels of a problem representation. Indeed, in order to solve an arbitrary ill-structured problem, we should be able to generate a completely new system of distinctions, containing as well goals, operators, problem-states, predicates as objects. Hence we must generalize the variation-selection dynamics in order to describe change at all levels of a representation.
4. Towards a Dynamics of Distinctions.
Suppose now that we would have a workable generate-and-test scheme for constructing and ameliorating representations. Then we could apply this scheme to itself in order to make it more efficient. This is a peculiar characteristic of metarepresentations : a metarepresentation allows to manipulate representations, yet it is itself a representation ; hence it can manipulate itself (cfr. Pitrat, 1986; Lenat, 1983; Newell, Shaw & Simon, 1960). This argument can also be used to explain why it is meaningless to look for a meta-metarepresentation, a meta-meta- metarepresentation, etc. Indeed, such higher level representations could only be used to reason about representations (from whatever level) and hence would not be in any way more powerful than the (second level) metarepresentation. By using this self-representing feature of metarepresentations we can now speed up the process of developing a metarepresentation through a bootstrapping procedure.
Indeed, one way to approach the construction of a metarepresentation, i.e. a representation of all possible ways of generating a problem representation, is by applying the general analysis of representation systems we have made (fig. 1) at the metalevel. The elements of the lowest level of our metarepresentation, the meta-objects, correspond to distinctions. The next level, the meta-predicates, is formed by the different classes according to which the distinctions can be categorized : the class of goal distinctions, the class of operator distinctions, ... , and by the (as yet not clearly defined) relations between distinctions belonging to these classes. The meta-states correspond then to systems of distinctions, structured by the meta-predicates. For the meta-operators, we need production rules which would be able to generate new structured sets of distinctions. The highest level of the metarepresentation, the meta-goals and meta-values, would then correspond to criteria for evaluating whether a particular meta-state, i.e. a distinction system, would be more or less adequate for representing a particular problem domain, which is defined by the relation between the autonomous agent and its environmental situation.
This description provides us with a first, relatively well-defined formulation of the problem of problem-formulation. However, in order to make the problem really well-structured, so that its resolution can be approached by simple search, we need a further explicitation of the different meta-structures. The least explicit levels until now are the two highest levels, which determine the dynamics of distinction systems.
In our definition of a problem representation, we have assumed that a problem is determined by two factors external to the representation itself : the autonomous agent, and the situation as he experiences it through his sense organs. This means that two sets of distinctions are given a priori : the survival-destruction distinction for the agent, and the set of distinguished stimuli (fig. 1). This last set is normally very large, and can be used as a basis for generating new distinctions by the combination (intersection, union, complement) of classes of stimuli. Roughly speaking, if the set of distinguishable stimuli has cardinal number N, the set of distinctions which can be generated corresponds to the power set of the set of stimuli, and thus has cardinal number 2N. This number is so large that for all practical purposes it can be considered to be infinite. (in fact, if we consider operator distinctions as functions mapping classes of stimuli to classes of stimuli, then the number of possible operators is even larger).
It is clear then that the variety of potential distinctions to be generated is extremely large. The difficulty resides in the selection of the most adequate distinctions. Ultimately this adequacy is determined by the capability of the distinction system to ensure the survival of the agent, i.e. to ensure that the agent will not be eliminated by natural selection. Hence there is an a priori selection criterion, determined by the relation between the agent and its environment. This criterion is based on the stability, homeostasis, capability of counteracting destructive perturbations, ... , of the agent. However, this criterion can only be applied in a very indirect way to the selection of representational distinctions.
We hence need "mediating" criteria, which would connect the representational distinctions to the survival-destruction and physical stimuli distinctions. One way to define such a "vicarious" selection criterion (cfr. Campbell, 1974), is by replacing stability with respect to the physical environment by stability with respect to the representational environment of already given distinctions. A distinction could be considered stable in this sense if it would be conserved by all representational operators, functions or relations, i.e. if it would be continuously connected to the other distinctions (continuity can indeed be defined as the conservation of topological distinctions, cfr. Heylighen, 1987a).
This mediating selection can be further structured by arranging the vicarious selectors in a hierarchy (cfr. Campbell, 1974), related to the distinction hierarchy (fig. 1), so that each potential new distinction would be selected first by the distinctions of the two contiguous levels. For example, a new goal distinction would be positively selected if : a) if reaching this goal would imply survival (level above); b) if this goal could be reached by a sequence of already given operators (level below). A predicate distinction would be selected if : a) it would allow to distinguish already distinct objects (level below); b) if it would allow to generate existing state propositions. A state distinction would be selected if : a) it would be the result of applying an existing operator to an already existing state; b) if it would correspond to a new combination of existing predicates. It is clear that these selection criteria have to be worked out further, and in particular that their mutual relation has to be specified.
5. A Transdisciplinary Research Project.
To tackle such a broad problem like the development of a metarepresentation it seems advisable to integrate methods from different disciplines, thus defining a transdisciplinary research project : 1) a conceptual-philosophical approach; 2) a formal-computational approach; 3) an experimental-psychological approach. (Such a project, involving researchers from different disciplines, is to be started at the Free University of Brussels (VUB). Although the present paper attempts to develop a general conceptual framework for this project, the views espoused here engage only the author ; they do not represent the group as a whole.)
The first approach would involve a theoretical analysis of the different concepts related to representation development : e.g. agent, situation, goal, object, ... This analysis could be based on existing theories, such as systems theory, theories of self-organization, epistemology, psychological theories of cognitive development, artificial intelligence models of learning and discovery, cognitive modelling, frameworks for representation in logic, mathematics and physics, ... The result of this analysis would be to provide fundamental definitions of the concepts in terms of more primitive concepts (e.g. the concept of distinction). For example, a proposition, or Boolean distinction, might be defined as a distinction which obeys the two axioms proposed by Spencer-Brown (1969) (cfr. sect. 2). The procedural interpretation of these (declarative) definitions would correspond to a program for constructing a more complex concept (e.g. an algebra of propositions) out of more primitive concepts.
This brings us to the second approach : the set of definitions can be read as a formal system, consisting of "facts" and "rules". (A provisional formalism for the deduction of classical and non-classical representations from a general distinction-based framework can be found in Heylighen, 1987a). These facts and rules could then be translated in a logic programming language (e.g. PROLOG), and implemented on a computer. The resulting program would correspond to an expert system, or rather to a meta-expert system, which would allow to infer higher-order distinction systems (i.e. representations) from ill-structured sets of primitive distinctions. The previous approach could hereby be considered as the preliminary phase of "knowledge acquisition" or "cognitive systems analysis", which collects and structures the "expert knowledge" to be implemented. A possible application of such a program might be the processing of existing expert systems, where a relatively unstructured list of facts (predicative propositions) and rules would be given as input, and where the output would consist of a well-organized, transparent and efficient, quasi-classical representation.
The function of the third approach would be to provide impulses and feedback for the general project, by comparing the theoretical-computational models with observations of real-world phenomena. In order to achieve this, a psychological experiment would be set up, in which experimental subjects would be asked to tackle an ill-structured problem (e.g. a simulation of the administration of a town (cfr. Dörner et al., 1983) or the management of a third world country (cfr. Dörner & Reither, 1978)). They would be provided with a set of primitive distinctions determining the perceived data ("stimuli"), and the fundamental distinction to be maintained ("survival", e.g. of the town organization). Through direct observation, protocol analysis, Kelly grid techniques and interviews the observer would study how the subjects would structure the problem, which goals, operators, states, predicates, objects, ... they would distinguish, and how these representations would evolve under the influence of learning, feedback, and reflection. This process and its results could then be compared with the expectations derived from the theoretical and computer models, allowing to correct them if necessary.
References.
Amarel S. (1968) : 'On Representations of Problems of Reasoning about Actions', in : Machine Intelligence 3, D. Michie (ed.) (American Elsevier, New York).
Burghgraeve P. (1976) : 'On Representations of Problems in Heuristic Problem-Solving', Communication & Cognition 9, p. 231
Campbell D.T. (1974) : 'Evolutionary Epistemology ' , in : The Philosophy of Karl Popper, Schilpp P.A. (ed.), (Open Court Publishing, La Salle, Illinois), p. 413.
Dörner D. & Reither F. (1978) : 'Über das Problemlösen in sehr komplexen Realitätsbereichen', Zeitschrift für Experimentelle und Angewandte Psychologie 25.
Dörner et al. (1983) : Lohhausen : Vom Umgang mit Unbestimmtheit und Komplexität (Hans Huber Verlag, Berlin)
Heylighen F. (1986) : 'Towards a General Framework for Modelling Representation Changes', in: Proceedings of the 11th International Congress on Cybernetics, (Association Internationale de Cybernétique, Namur, Belgium).
Heylighen F. (1987a) : Representation and Change. An Integrative Metarepresentational Framework for the Foundations of Physical and Cognitive Science, (Ph. D. thesis, Vrije Universiteit Brussel).
Heylighen F. (1987b) : 'Formal Foundations for an Adaptive Metarepresentation', in : Cybernetics and Systems : the Way Ahead (vol. 2), J. Rose (ed.), (Thales publications, St. Annes-on-Sea, Lancashire), p. 648.
Heylighen F. (1988) : 'Autonomy and Cognition as the Maintenance and Processing of Distinctions', in : Rosseel, Heylighen & Demeyere (1988).
Hobbs J. (1985) : 'Granularity', in : Proceedings of the 9th International Joint Conference on Artificial Intelligence(vol. 1), p. 423.
Korf R.E. (1980) : 'Toward a Model of Representation Changes', Artificial Intelligence 14, p. 41.
Lenat D.B. (1983) : 'EURISKO : A Program that Learns New Heuristics and Concepts,' Artificial Intelligence 21, p. 61.
Newell A., Shaw J. & Simon H.A. (1960) : 'A Variety of Intelligent Learning in a General Problem Solver', in : Self Organizing Systems, Yovits & Cameron (eds.) (Pergamon Press), p. 153.
Newell A. & Simon H.A. (1972) : Human Problem Solving, (Prentice-Hall, Englewood Cliffs)
Pitrat J. (1986) : 'GPS utilisé comme programme d'apprentissage pour GPS', in : Sciences de l'Intelligence. Sciences de l'Artificiel, Demailly A. & Le Moigne J.L. (eds.) (Presses universitaires de Lyon), p. 51.
Rosseel E., Heylighen F. & Demeyere F. (eds.) (1988) : Self-Steering and Cognition in Complex Systems. Toward a New Cybernetics, (to be published by Gordon & Breach, New York, ).
Spencer Brown G. (1969) : Laws of Form, (Allen & Unwin, London).