
BUILDING A SCIENCE
OF COMPLEXITY
Francis HEYLIGHEN[1,2]
ABSTRACT. It is argued that in order to solve complex problems we need a new approach, which is neither reductionistic nor holistic, but based on the entanglement of distinction and connection, of disorder and order, thus defining a science of complexity. A model of complex evolution is proposed, based on distributed variation through recombination and mutation, and selective retention of internally stable systems. Internal stability is then analysed through a generalized mathematical closure property. Examples of closure in self-organizing and cognitive systems are discussed.
1. Introduction
It is a common observation that our present society is more complex than any of the societies or cultures which preceded it. This entails that the problems this society, and the individuals who are part of it, must confront are more complex than they ever were. Understanding complexity seems to be the only possibility for escaping this evolution in which everything seems to become more uncertain, more complicated and more changeful.
In order to analyse scientifically what complexity is, we should begin by giving a more intuitive account of what the word "complexity" denotes. First, we would call a system "complex" it is has many parts or elements. However, sheer quantity is not sufficient : we would not see a brick wall as being complex, even though it is composed of thousands of different bricks. Moreover, the way the elements are aggregated should be in some sense disordered or unexpected, it should not be reducible to a regular, periodic pattern, like the bricks in a wall or the molecules in a cristal. This "unexpectedness" becomes even more apparent in the dynamics of the complex system : it we interact with the system, or if it evolves on its own, the changes which we experience are unpredictable. Moreover, they are in general also irreversible. We cannot control or steer the evolution of the system. This entails a third basic feature of complex systems: the anticipation or management of a complex systems behaviour defines a problem which is difficult, if not impossible, to solve.
Problems such as pollution, underdevelopment, war, diseases like AIDS, ..., are examples of such complex situations, which are extremely difficult to cope with, because of the quantity and irregularity of all the factors involved, which makes it practically impossible to anticipate the effects of proposed interventions (cfr. Dörner, 1983; Dörner & Reither, 1978; Heylighen, 1988). The only general method for solving difficult problems we know is science. However, traditional science often seems to create more problems than it solves. Problems such as pollution or the threath of nuclear warfare would not exist without science and technology. Moreover science only appears capable of solving problems in very specialised, restricted domains, while ignoring problems on the level of the planet or of the society.
This may be understood by observing that the domains of classical science are chosen such as to avoid complexity as much as possible. Let us consider Newtonian physics, which is the mother discipline defining the mechanistic paradigm, which has influenced most of the other sciences. The objects of physics are typically modelled as particles, as elementary systems without internal structure which obey invariant, external laws of motion. Even when a physicist considers a planet, he sees it as a rigid, spherical ball which moves around the sun in a trajectory determined solely by its global mass, ignoring all chemical, biological, psychological or cultural systems which may have developed on the planet. Of course the physicist is aware that he neglects a lot of important phenomena when he models the planet as if it were a particle. Nevertheless, a traditional physicist remains reductionistic : he believes that all the behaviours of all the complex systems on the surface of the planet, be they geological or social, can be understood through the mechanics of the elementary particles by which they are constituted.
One of the basic problems with this philosophy is that it entails that all apparently complex phenomena can be reduced to combinations of fundamentally simple elements and interactions, and that it suffices to describe these elements in sufficient detail in order to obtain a complete and deterministic model of the complex phenomenon, which should in principle allow to solve all problems about the phenomenon. The aim of physics can then be formulated as a search for the most complete possible description of the most elementary phenomena. However, the evolution of physics, first with quantum mechanics, then with quantum field theories and now with the most recent elementary particle theories, has shown that this search leads to models which become ever more complex. It seems as though the more elementary the level of analysis, the larger the number of particles and fundamental constants needed, the more complicated the structure of the theory, and the more uncertain the predictions derived from it. Clearly something has gone wrong with the program of constructing as complete as possible representations of as simple as possible phenomena.
In this paper I want to argue that a quite different approach is needed in order to understand complexity. First, you should not try to reduce complex systems to simple elements, but try to understand complexity as an overall feature. Second, you should not attempt to find a complete representation, but acknowledge that since a representation is necessarily incomplete, it is most appropriate to search for that representation which is as simple as possible, given the problem you want to solve. Such a research philosophy would define a new discipline : the science of complexity (cfr. Banathy, 1984; Mesjasz, 1988).
Of course this new science would not have to emerge out of nothing : there are several approaches which have already much contributed to the analysis of complexity (cfr. Vullierme, 1987), and which may hence be used as a basis on which a more elaborated, integrated theory may be build. One of these approaches is formed by cybernetics and systems theory (in practice it seems impossible to draw a boundary between the two), whose subject is the study of the behaviour of general (complex) systems. However, what is lacking in this approach in order to to make it a full-fledged theory of complexity is a model of how a system, and complexity in general, may emerge out of something which is not yet a system. Such a phenomenon might be understood with the help of some recent concepts developed around the phenomenon of self-organization. A third strand we need for our general science of complexity concerns the way in which complex, autonomous beings, such as we ourselves are, may solve the problems posed by a complex environment. Such coping with complexity demands intelligence, and this leads us to the disciplines which have studied intelligence : cognitive science and artificial intelligence.
I shall now sketch a possible way in which the main ideas of these three approaches may be unified. But first I must try to define complexity in a more profound way.
2. What is complexity ?
Let us go back to the original Latin word complexus, which signifies "entwined", "twisted together". This may be interpreted in the following way: in order to have a complex you need : 1) two or more different parts or elements; 2) these parts must in some way be connected or knotted together, so that it is difficult to separate them. Here we find the basic duality between parts which are at the same time distinct and connected. Clearly a complex cannot be analysed or separated into a set of independent elements without destroying it. Hence we must conclude that the reductionistic method cannot be used for understanding complex entities. This accounts for the connotation of difficult, which the word complex has received in later periods. Indeed the general rational method of tackling problems consists in analysing the problem domain. If this domain is complex, then by definition it will resist analysis.
The awareness that there are phenomena which cannot be reduced to their separate parts, has led to a philosophy which may be seen as the opposite of reductionism, and which is called holism. This approach proposes to look at a complex phenomenon as a whole, instead of as a collection of parts. However, this view too neglects an essential feature of complex entities, namely that they are composed of distinguishable parts, even though these parts may be tied together. To consider a phenomenon as a whole means that you see it as one, i.e. as basically simple.
In the limit the holistic position would entail that, since the universe consists of one network of interconnected systems, any form of analysis leading to distinct objects or systems is to be excluded. This would imply that the only way we can gain any real knowledge about the world would consist in mystical experiences during which the boundaries of self and cosmos are transcended (so-called mystical union or nirvana). Although I do not want to exclude that such experiences may be quite enriching for the individual who undergoes them, I think it is clear that they cannot in any way constitute a "scientific" method for solving the problems posed by the complexity of the present world.
We must conclude then that in order to build a science of complexity we can rely neither on the reductionistic position nor on the holistic position. The study of complexity demands a transcendence of the holism-reductionism polarity. We need an approach which allows to model systems which are both distinct (and hence in an abstract way separable) and connected (and hence cannot be separated without losing part of their original meaning).
Perhaps the simplest way to visualize a model which would satisfy these two seemingly contradictory requirements is to consider the (mathematical) concept of a network. A network consists of nodes, usually represented as points, and connections between nodes, usually represented as arcs or arrows leading from one point to another one. The nodes can be viewed as the distinct parts of the complex network (= plexus), the connections as the relations which braid these elements together. (Remark that inversely the nodes can be viewed as connections, tying together the arrows, whereas the arrows can be viewed as distinct elements.)
The reductionistic approach may now be formulated most simply as a method which tries to eliminate as much as possible the connections, whereas the holistic approach eliminates as much as possible the distinctions between the nodes. In this sense both methods "reduce" a complex phenomenon to a basically simple entity (either a set of nodes or an undifferentiated whole) by neglecting an essential part of its features.
We may now also understand why the interaction with a complex system is so difficult. Assume that an influence is exerted on one of the parts (e.g. a node) of the complex. Through the connections this influence will propagate to the other nodes. However, since the nodes have distinct positions or functions in the network, each of them will react in a different way. Moreover, without analysing the network in detail and hence destroying it, we cannot have a complete knowledge of how each will react. This means that in general we cannot predict how a complex system will react to any influence, originated by the observer, by the environment or by its own dynamics. Equivalently, we cannot retrodict or reverse its evolution either, i.e. we cannot reconstruct its past by collecting information about its present behaviour.
This picture of complexity I just have sketched may appear too pessimistic. Indeed we know through the practice of science that in many cases we can make predictions which are more or less accurate. To understand this we must introduce a further concept : order.
3. In between Order and Chaos
Complexity is often taken to be a synonym of disorder or chaos. However, I want to argue here that disorder alone is not sufficient to define complexity. Let us therefore analyse what is meant by order and disorder.
The examples of order which come most easily to mind are symmetric structures, e.g. cristal lattices. Symmetry is defined mathematically as invariance under a group of transformations. In the same way order may generally be defined as invariance under some set of operations or transformations (not necessarily a group). The main characteristic of an ordered system is its (spatial or temporal) predictability. Indeed it suffices that we know a (spatial or temporal) part of the system to which we may apply one the invariance transformations. Because of the global invariance of the system we know that the result of applying an operation to one part of the system will produce another part of the same system. In this way we may reconstruct the complete system by applying all transformations to one well-chosen part. We do not have to know the system as a whole in order to reconstruct or predict its structure : the system is redundant.
Let us extend this definition of order to the limit, i.e. let us try to define a maximally ordered system. Such a system would be characterized by the fact that it would be invariant under all imaginable transformations. Obviously, the only possible structure for such a system would be characterized by perfect homogeneity : it should be possible to map any part of the system to any other part without any change occurring. Moreover, it should also have an infinite extension, because otherwise we could imagine transformations which would map a part of the system to some element outside its boundaries. In other words, such a perfectly ordered system would correspond to a classical vacuum, i.e. to an infinitely extended "substance" in which no part or internal structure at all could be distinguished. Clearly, such a system would be the opposite of what we have called a complex system, characterized by internal differentiation.
Let us now look at the other end of the order-disorder scale. Disorder is characterized by the absence of invariance, by the absence of (non-trivial) transformations which would have no distinguishable effect upon the system. In the limit this means that any part, however small, of the system must be different or independent of any other part. An approximate example of such a system would be a perfect gas : generally speaking the velocities of two different gas molecules will be distinct and independent; there is no coordination whatsoever between the different molecules. However, if we look more closely, there are invariances characterizing a gas cloud : the movement of one gas molecule is continuous during the short time interval in which it does not collide with other molecules; it is characterized by conservation of momentum. Moreover, the space in between the molecules can be viewed as a classical vacuum, which as we have seen is ordered.
In a maximally disordered system, on the other hand, we should have particles of any momentum appearing and disappearing at any instant in time and at any position in space. An example of such a weird system is the vacuum as it is seen in quantum relativistic field theories : the "quantum fluctuation of the vacuum" continuously creates and destroys virtual particles. These particles are called virtual because they are so unstable that it is in principle impossible to observe them. In practice this means that a quantum vacuum cannot be distinguished by observation from a classical vacuum. This leads me to conclude that both perfect order and perfect disorder in the limit correspond to emptiness, i.e. to absence of structure or differentiation, and hence to the absence of any form of complexity.
It is clear then that in order to have complexity we need some kind of mix of order and disorder, i.e. we need a system characterized by certain, partial invariances, which, however, are not global or absolute (cfr. Fig. 1).
The partial invariances may be viewed as some kind of connections between parts of the system which make these parts indistinguishable : the transformation mapping the one part onto the other one does not result in any observable change; the parts are assimilated or integrated. The complement of these relative invariances or assimilations, i.e. the disorder component, can then be viewed as a variation, a distinction between parts, so that the mapping of the one part onto the other one would result in an unambiguous change of the overall structure; the parts are distinguished or differentiated.

Fig. 1 : a complex pattern, characterized by an entanglement of order (rotational
and mirror symmetry) and disorder (randomly drawn lines).
4. The dynamics of complexity
A following step in the analysis of complexity should be an examination of how a complex system evolves, how it changes in time. The limited invariance we have postulated does not only apply to spatial or geometrical transformations but also to temporal or dynamical transformations. This means that certain "parts" or structures of the complex will be conserved during a given time evolution, whereas other ones will change. Until now this description sounds rather trivial : part of the system changes, part of it does not change. In order to have an interesting theory we should need some method for determining which of the subsystems will change, and which will not. I will try to show that such a criterion may be derived by reformulating this apparently trivial proposition.
Complex evolution according to the present view is characterized by an inextricable entanglement of disorder or variation, and order or invariance. Assume that we have a substructure of the complex which is relatively invariant, i.e. a (large) set of transformations does not affect it. This means that as long as the processes inside the complex belong to this category of transformations the substructure will remain. In other words the larger the class of transformations the more stable the substructure. Substructures which have a smaller set of invariance transformations will change more rapidly, they will survive during a shorter period. The more stable substructures are hence in some way selected : they survive while the other ones disappear. Hence we may reformulate complex evolution in the same way as Darwinian evolution in biology : on the one hand there is variation which continuously creates new structures, on the other hand there is some form of "natural" selection which weeds out the unstable structures and retains the stable ones.
But who carries out the selection? In biological evolution, the selecting agent is considered to be the environment which demands a certain form of adaptation of the system, otherwise the system cannot survive. If we study complexity in general, however, without making any a priori distinction between an organism and its external environment, we cannot use such a criterion. The distinction between subsystem which tries to survive and the environment which may allow or hinder this survival is itself only one feature of the complex system considered as a whole. Speaking about survival of one subsystem within the larger whole entails that we have some way to recognize such an invariant subsystem within the evolving complex. In other words the stable subsystem must be distinguishable as an individual, it must have an identity. The variation-selection dynamics is really a principle about the relative invariance of distinctions within a complex.
Let us then elaborate the principle of variation and selective retention from this point of view. By definition a complex consists of distinguishable substructures which undergo variation. Since the variation is not absolute or complete (otherwise we would be in the situation of the quantum vacuum) these substructures will have a minimal invariance or stability. This means that they will not change all at the same time : there is some form of inertia or continuity which limits change. This allows us to concentrate on one substructure and to consider it as having a stable identity (i.e. distinction) during a limited (perhaps infinitesimal) time interval. What may then change during this interval? Either the relation or connection between this substructure and the other ones in the complex changes, or the internal organization (i.e. the relation between its parts) of the substructure changes. The first process may be called (re)combination of substructures, the second one mutation of the individual substructure.
These processes may be illustrated by the genetic variation processes inside biological systems : consider a chromosome as an example of a stable substructure; recombination then corresponds to the process by which a chromosome is separated from the one it forms a pair with, in order to be coupled again with a chromosome of another organism during sexual reproduction; mutation corresponds to the changing of one or more individual genes within an invariant chromosome.
The usefulness of this distinction between recombination and mutation resides in the fact that these processes can in general be separated : they happen on a different time scale, and have effects on different levels of the complex. If the substructure is intrinsically very stable, then the process of mutation will be very rare or unlikely, whereas the process of recombination may happen continuously without affecting the survival of the substructure.
Both processes however lead to variation which in turn may lead to new, selectively retained substructures. In the case of recombination these new structures will appear on the level of the larger system of which the original substructure forms only a part. In the case of mutation the new structures will themselves be parts of the original substructure. Both processes may have an effect on the further maintenance of the original substructure.
What we need now is a general stability criterion which would allow us to predict whether a new structure created by variation would be likely to survive. As we already remarked such a criterion should not depend on a mysterious, because external, environment : it should be internal to the evolving complex itself. In the remainder of this text I will introduce the concept of closure, which allows us to define such a criterion.
Consider now a complex whole consisting of a large number of substructures which are partly evolving in parallel with each other, partly overlapping, partly in part-whole relations with each other. The emergence of new stable substructures (in general at different levels) in this complex can be seen as the development of a new internal organization. This development is not determined by an external agent or environment, but only by the internal variation processes and selection criteria. It hence corresponds to what is called self-organization.
Remark that this evolution will in general lead to more complexity. Indeed, assume that the system is originally relatively simple, i.e. there are few distinct and invariant structures. By selective stabilization invariant structures may emerge. These stable structures will now themselves form building blocks which by combination may give rise to higher-order stable structures. These higher-order structures themselves may then form the building blocks for even higher-order structures. The process of constructing invariant structures by stabilization of specific combinations of already stabilized substructures is indeed a recursive process, which is unlimited in its power to engender ever more complex structures. This recursivity argument is comparable to Simon's (1962) explanation for the hierarchical organization of spontaneously evolved complex systems.
5. Cognition as adaptation to complexity
In order to explain cognition we must start from a factorization of complexity into an autonomous system and its environment. An autonomous system is a stable substructure, whose stability is not only due to its internal stability (i.e. the invariance of the system under its internal processes or transformations), but also to its capability of actively resisting external perturbations. Consider for example a stone as a system which its stable due to the rigidity of its internal, cristalline structure. This structure is strong enough to resist most outside influences, e.g. pressure or temperature change, the force of gravitation, etc. However, if the externally applied influence is strong enough (e.g. heating to 8000 deg. C), the structure will be destroyed automatically.
A biological organism, on the other hand, may be less rigid, but more adaptive, in the sense that it will change its internal functioning in such a way that external perturbations are compensated. The eventual destruction of the system is not automatical but depends on the capability of adaptation, of counteracting external influences by internal changes. A system which can thus maintain its identity by active adaptation may be called autonomous (cfr. Heylighen, 1989).
This adaptive capability depends on two things : 1) the system must dispose of a set of adequate responses or actions, which can eliminate a large variety of perturbations; 2) the system must be able to choose that combination of actions in the set which is appropriate for the given perturbation. We will assume that the primitive actions needed for (1) are given, are determined by the systems physical structure (which in the case of biological systems is determined during evolution). We then remain with problem (2), which, however, is far from trivial.
Even when the set of primitive actions is quite small, the set of possible adaptive behaviours (defined as sequential or parallel combinations of primitive actions) is in general infinite. (this may be compared to linguistic competence : although the set of words and grammatical rules in a language is finite, the set of all possible grammatical sentences is infinite.) By going from primitive actions to action combinations not only the amount of possible choices grows drastically, also the potential power increases dramatically. For example, although the primitive actions a human being is capable of (e.g. walking, talking, grasping, ...) are rather unimpressive, one individual, by producing a specific combination of such actions, may create a situation in which he can destroy the world by pushing a button (and thus starting a nuclear war).
It is clear then that the problem of choosing an appropriate combination of actions is very complex. In order to make such a choice the autonomous system (or actor) must dispose of a special kind a competence : it must know which effects a given environmental perturbation or internally selected action complex will have. This knowledge can be modeled as a complex structure : a cognitive system.
The effects of a combination of actions will of course depend on the structure of the environment, and so the more complex the environment, the more complex the knowledge the actor needs. Indeed the more distinct perturbations the environment can generate, the larger the variety of distinct action complexes the system must be able to respond with. This is just a paraphrase of Ashby's "Law of requisite variety".
However, we must also be aware of another basic requirement : in general a perturbation must be counteracted within a relatively short time, otherwise the system may be destroyed before it has taken the apppropriate action. In order to find the appropriate action the system must somehow carry out a search through the space of all possible action complexes. Since, as we have argued, this space is generally infinite, the search process may take a very long time. The only general method to restrict the expected duration of the search consists in keeping the structure of this space as simple as possible, so that the number of alternatives to be explored at each decision point in the search graph, and the expected number of decision points would be minimal. In other words the variety of distinct alternatives and of distinct decision steps should be minimal. We may conclude that the cognitive system should be of minimal complexity. In practice this means that the cognitive system should be less complex than the environment whose changes it tries to anticipate (Heylighen, 1987).
Synthesizing the two arguments we may conclude that the cognitive system an actor needs for finding the appropriate responses to the environmental perturbations must be minimally, yet sufficiently complex. This means that the cognitive system will consist of distinct yet connected parts, such that the number of distinctions is on the one hand large enough for coping with the variety of possible perturbations, on the other hand as small as possible.
Let us now analyse how such a cognitive system might develop. Like all complex systems its evolution may be seen as self-organization, based on a distributed variation-and-selection process. The difference with an ordinary complex system, however, is that the selection should pick up structures which are not only intrinsically stable, but whose overall organization should be as simple as possible, given the variety of perturbations they must be able to cope with. In other words the cognitive selection criteria should restrict the amount of internal details, within the given constraints. These constraints are determined by the stimuli the system receives from the environment and by the vulnerability of the actor with respect to the environmental perturbations. This means that the system should only distinguish between patterns of stimuli if this distinction would have an effect on its overall vulnerability, i.e. on its chances for long-term survival. In other words two patterns should be distinguished if they would correspond to different perturbations, or would induce different actions for coping with perturbations. The interpretation of patterns in terms of future perturbations or actions entails that these patterns would correspond to phenomena with a minimal stability. Hence the cognitive distinctions should be such that they allow to recognize relatively invariant patterns. This gives us more information about an eventual cognitive selection criterion. We will now propose a fundamental concept : closure, and argue that it provides a basis for constructing general selection criteria for the evolution of complex systems, as well general as cognitive systems.
6. Closure as an internal invariance criterion
Closure is a well-known concept in systems theory : a system is called closed if it does not interact with its environment, if it has no input or output. Clearly, a closed system thus defined is not a very realistic thing : all systems somehow interact with other systems, otherwise we would not be able to observe them and it would be as if they did not exist at all. Moreover, our definition of complexity excludes systems which are not connected in some way to other systems. Yet closure is a very useful concept because it allows to simplify descriptions. Therefore we will try to propose a more general definition of closure, inspired by mathematics, which would still be useful for modelling complexity. This concept would also be a generalization of the concept of "organizational closure" used by Maturana and Varela (1980; Varela, 1979).
The basic idea is that only certain classes of interactions would be excluded, but not all of them. According to the variation-selection dynamics, the interactions which should be excluded are those which prohibit the further existence of the system, which destroy its invariance. As we have noted earlier, we are primarily interested in internally determined invariance, i.e. by selection carried out by the system itself, not by its environment.
The first question we should ask is : what should remain invariant? Clearly it is not realistic to require that any part or feature of a system, any of its elements, attributes and relations, be conserved during evolution. Complex systems do undergo changes, yet somehow they may maintain their identity. It is this "identity" which should remain invariant. This identity can in general be defined as a distinction between the system or structure, and all those other phenomena which do not form part of the system. So we are looking for invariant distinctions. This means that we need a set of transformations or operations which would map the distinction upon itself, while possibly changing other features of the system or its environment. These transformations should be internally determined, belong to the internal dynamics of the system. Let us then advance a general definition :
a system is closed if all the transformations arising from its internal organization are such that they map the distinction (or set of distinctions) defining the identity of the system upon itself.
The traditional illustration of an identity determining distinction is a topological boundary, which separates the inside elements from the external ones. However, the definition allows much more general distinctions. For example, the geometry of space can be considered as a mathematical system, containing a set of symmetry transformations (e.g. translations and rotations) which keep invariant a certain number of defining distinctions, for example the dimensionality of space. In other words the distinction between one dimension and the other ones is mapped upon itself by the transformations contained in a geometrical system.
Another example might be the causal structure of relativistic space-time, determining the distinction between slower-than-light and faster-than-light connections between events and thus the partial order structure of time, which is invariant under Lorentz transformations. Hence even time itself may be considered as a closed system, defined by the invariant distinction between future and past.
In order to clarify the significance of these rather abstract examples we should try to understand in more detail what is meant by a system and the transformations contained in it. A system can in general be defined as a relation between an input set and an output set (Mesarovic and Takahara, 1975), it "maps" in a certain sense inputs to output. Hence a system itself may be considered as a transformation. The transformations "contained" in a system are then simply its subsystems. The notion of transformation as we use it here, however, is more than purely dynamical. The transformation might be an abstract relation between variables, without representing a "process", characterized by time or duration.
Let us consider another, more concrete example : a cristal. A cristal is characterized by its symmetrical structure, i.e. by the invariance of the pattern of connections between its elements (molecules) under a certain group of translations and rotations. These transformations do not correspond to actual physical processes happening inside the cristal, but to spatial relations between molecules, e.g. the relation between a molecule and the one which is immediately left of it. This relation, however, has a physical meaning : it corresponds to a chemical bond between molecules, which forms a rigid connection. It is just the presence of such a "symmetrical" set of relations which makes the cristal a stable structure, compared with a random assembly of molecules.
You may have noticed that all the examples of closed systems of transformations or relations considered until now correspond to mathematical "groups", i.e. algebraic systems characterized by associativity, internality of composition and the existence of identity and inverse elements. The property of closure is more general than that, however, although a group is a very good example of a closed system, because it combines several elementary closure properties. Let us look at them one by one.
The most basic perhaps is the internality of composition: this means that any two transformations or relations of the system may be sequentially composed, so that they form a third transformation which is still part of the original system. In other words the system is invariant under the composition of transformations. This basic type of closure may be called transitive or recursive closure. If we make the set-theoretic union of all the relations in the system then the resulting relation must be transitive.
Another fundamental closure is implied by the existence of symmetrical or inverse transformations. This means that the system is invariant under the inversion of transformations. In practice it signifies that if you apply a transformation to an element, you may always reverse the effect of this transformation by applying the inverse transformation to the resulting element, thus going back to the original element. This may be called symmetric closure. It is a special case of a more general type of closure : cyclic or circular closure, which states that any sequence of transformations may be inversed by applying another specific sequence of transformations to its result, so that the concatenation of both sequences defines a "cyclic" path (without thereby assuming that each individual transformation would have an individual inverse).
Implicit in the concept of a group is the idea that a transformation would correspond to a bijective mapping, i.e. a relation which is one-to-one. However, in general a relation may also be many-to-one, one-to-many or many-to-many. The restriction of a many-to-many relation to a many-to-one (i.e. surjective) relation (or equivalently, to a one-to-many relation) can again be understood as a closure of the relational system. Indeed, a many-to-one relation R is characterized by the fact that the composition of the relation with its inverse R-1 gives an identity :
R[ R-1 [ a]] = a, for all a.
Equivalently for one-to-many :
R-1[ R [ a]] = a, for all a.
In the case of a one-to-one relation, both properties apply. Hence the initial input or output elements to which the relations are applied are invariant under the transformations R o R-1 and/or R-1 o R, and hence may be considered to form a "closed" system. A one-to-one mapping may be characterized by the fact that it conserves all the distinctions between elements: distinct elements are sent upon distinct elements. These properties may be called respectively surjective (many-to-one), inverse surjective (one-to-many) and bijective (one-to-one) closures.
We have thus defined four basic types of closures : transitive, cyclic, surjective and inverse surjective. (bijective and symmetric closures are special cases of these general classes). The fact that these closures are really fundamental can be understood by looking at a very simple diagram consisting of two connected arrows representing two relations or transformations. Closure may then be represented by the addition of a third arrow, so that the resulting diagram is "closed". One can easily see that there are four inequivalent ways in which such a three-arrow diagram may be closed, leading to the four types of closures defined above (Fig. 2 and 3).
In the first two diagrams (Fig. 2) the two original arrows (in plain line) are sequentially connected, i.e. such that, with respect to their common node, one is ingoing, the other one is outgoing. The third arrow (in dashed line) which is added for closure can be oriented in two ways: either in continuation of the sequence of two arrows, thus leading back to the starting node (first drawing, cyclical closure) or in parallel with the sequence (second drawing, transitive closure). In the second two diagrams (Fig. 3) the two original arrows are connected in parallel. Because of the overall symmetry this means that the connection to be added for closure must be non-oriented (arrows in both directions). Such a symmetric connection can be interpreted as an equivalence relation, leading to the identication of the two connected nodes, so that they are no longer individually distinguished but only as a collection. The result is that also the original arrows are no longer distinguished, so that the relation formed by theses arrows becomes inverse surjective (one-to-many), respectively surjective (many-to-one).
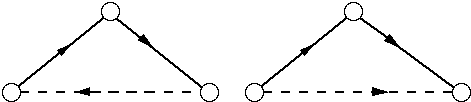
Fig. 2 : a cyclic, respectively a transitive closure of a 2-arrow graph
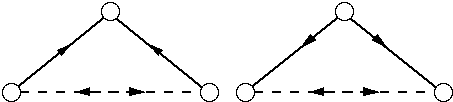
Fig. 3 : an inverse surjective, respectively a surjective closure of a 2-arrow graph.
We may add one more remark here : if we would use a four arrow diagram we could see transitive closure as related to what might be called commutative closure, requiring that the composition of two transformations be invariant under the permutation of the order in which the transformations are composed.
7. Some examples of complexes generated through closure
Let us sketch how closure could help us to understand the self-organization of a complex system. Any system can be viewed as a collection of interacting subsystems. These subsystems can be modelled as input-output relations. The interaction between these subsystems leads to the (re)combination of subsystems in temporary assemblies through variation. The coupling of the subsystems within an assembly may be understood in the following way : two subsystems A and B are coupled in sequence if the output of A is used as input by B; they are coupled in parallel if they use or produce the same input and/or output. Suppose now that the assembly of systems-relations is characterized by some form of closure. We may then hypothesize that the assembly would gain some form of internal stability and hence could be selected for survival. The assembly would then form a new, higher-order subsystem which could again be used as a building block for new recombination processes, which may again lead to closures.
It is clear that this provisional description is to be worked out in much more detail if we wish to construct a general, mathematical theory of complexity. This is work for the future. For the moment it will suffice to consider several examples of self-organizing processes, thus showing that closure can help us to understand their emerging structures.
In the case of cristal formation the subsystems might correspond to the relations of attraction between couples of molecules. Closure then sets in when by diffusion of the molecules these relations are able to form a symmetric pattern.
An example of self-organization where the creation of new distinctions is very clear is the formation of cracks in a previously smooth, homogeneous surface (see fig. 4). This phenomenon can be observed in the patterns formed by drying mud, or old paint on a wall. A crack can be seen as a local distinction, locally separating the two sides of the crack. Yet this distinction is in general not global or invariant : at the edges of the crack the separated sides come back together. However the distinction becomes invariant if the crack closes in on itself, so that one side becomes separated from the other side, leading to an "inside" and "outside", distinguished by a closed boundary.
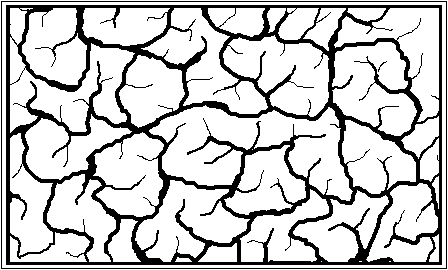
Fig. 4 : a complex pattern formed by cracks in a smooth surface.
Thermodynamical self-organization is usually modelled through the concept of "attractors" (Prigogine, 1979; Nicolis & Prigogine, 1986; cfr. also Kauffman, 1984). An attractor is set of states of a dynamical system such that if the system is in a state belonging to the attractor, then it will remain within this attractor. An attractor can in general be seen as a cyclically closed system of processes. This is understood most easily by looking at point attractors or one-dimensional attractors (limit cycles), where the system comes periodically back to its inital state. However, the closure of an assembly of processes does not necessarily require that there be an invariant periodically recurrent state : it suffices that there be an invariant distinction. This distinction corresponds to that between processes inside the attractor set (which by definition cannot get out) and processes outside. This allows us to understand multi-dimensional and even strange or chaotic attractors as closed systems.
Another example of a structure which appears to be typical for self-organizing complex systems is that exhibited by fractals or self-similar patterns (Mandelbrot, 1982). The recurrence of the same form at different levels can be understood as the result of the recursive coupling of one or a few primitive processes. This is an example of a transitive closure.
Yet another basic structure which is found again and again in naturally developed (and even artificially designed) complexes is hierarchy (Simon, 1962). This may be modelled mathematically by a tree structure, which can be seen as a network of surjectively (or equivalently : inverse surjectively) closed relations. The growth of plants shows that tree structures need not be abstract : even the concrete, visible world around us is filled with them.
This brings us to the organization of biological systems. A living system can in general be defined by its autopoietic organization : it consists of a network of processes which produces itself (cfr. Maturana and Varela, 1980; Varela, 1979). The typical example of this circular organization is the cycle through which the DNA in a living cell produces enzymes which themselves steer the production of new DNA, which again produces enzymes, ... This is obviously an example of a cyclical closure.
Autopoietic systems have the capability of cognition, and this brings us to the self-organization of cognitive systems.
8. Closure and cognitive structuration
As we have said, an autonomous system should be able to reconstruct the stable distinctions relevant for its survival out of the stimuli it receives; in other words, it must be able to extract meaningful (i.e. invariant and relevant) patterns out of the scattered stimuli (e.g. electrical impulses generated by light falling in upon the optical nerve).
This process has been studied by Gestalt psychology (Stadler & Kruse, 1989). Patterns which are perceived can be characterized as Gestalts, i.e. as coherent wholes, distinguished from their background. The qualities which make up a Gestalt can again be interpreted as closure properties, e.g. symmetry, continuity, invariance.
It must be emphasized that the closure which is perceived is not in the stimuli themselves, which are basically discrete or separate. The cognitive system "closes" the pattern by filling in the missing elements (Stadler & Kruse, 1989). For example, a set of dots arranged in the form of a triangle will generally be seen as a continuous figure, not as a collection of separate elements. In the same way the disappearance of a moving object behind a screen followed shortly thereafter by the appearance of a moving object at the other end of the screen will be automatically interpreted as a continuous movement of one and the same object, even though behind the screen the object might have been destroyed and replaced by a similar object. The cognitive system of the observer will again fill in the missing movement behind the screen and thus "close" the trajectory of the supposedly invariant object.
These examples show us that cognitive structures should not be seen as simple mappings of external physical structures by means of the sense organs. The physical stimuli merely "trigger" internal processes of self-organization characterized by closure. The meaning of the stimuli is really "constructed" inside the cognitive system. It is a well-known phenomenon in the psychology of perception that the same physical pattern of stimuli may be closed or interpreted in different, incompatible ways, and that this interpretation may shift in an abrupt manner, leading to the phenomenon of "Gestalt switches".
This phenomenon is analogous to the incompatibility of different modes of observation in quantum mechanics. For example the same electron may be seen either as a wave or as a particle. The observability of properties in quantum mechanics may again be modelled by a closure operation: orthogonal closure (see Heylighen, 1987) (this is an example of a surjective closure of a relation which is symmetric but not transitive).
The fact that the same entity can be perceived or modelled in incompatible ways is an argument against the idea that cognitive systems or internal representations may be modelled as homomorphic images of an "external reality". Even though there is a relation between environment and cognitive system, this relation is neither an isomorphism nor a homomorphism, it is not even a function. We may conclude that the closures inside the cognitive system do not necessarily correspond to the closures in the environment.
In order to be adaptive the cognitive system must of course provide as much "coherence" as possible between anticipations and perceptions, and thus it would be useful if there were some form of correspondence. However, this correspondence is necessarily incomplete since the invariant distinctions the actor needs for his survival are infinitely smaller in number than the invariant distinctions in the environment, because of the reduction of complexity needed for adequate problem-solving. Moreover these cognitive distinctions are basically subjective since their function consists in enhancing the actor's chances for individual survival. Hence it is natural that a cognitive system would make distinctions (by closing internal patterns) which do not correspond to any external, invariant closures, but whose only aim is to reduce the complexity of the problems posed by survival. For example, an actor will in general make a distinction between "good" events and "bad" events, although there is not any external, invariant counterpart of the class of all good things (such a class corresponds again to the "orthogonal" closure (Heylighen,1987) of a set of events : the class of all good events is equal to the class of all events which are not bad, i.e which are not "not good").
We may conclude that both the cognitive structuration of a complex pattern of stimuli and the structuration through self-organization of the physical system, which has caused these stimuli, can be understood with the help of the same basic principles of variation and closure. However we must note that the parallellism of these two self-organization processes does not lead to a global isomorphism or homomorphism of the resulting structures. The exact relation between the cognitive system and the physical system it models is itself quite complex. A further elaboration of the present model of complexity may help us to gain a deeper understanding of this extremely important phenomenon.
9. Conclusion
We have argued that in order to understand the complex problems of present-day society we need a fundamentally new approach, which would replace the reductionistic method of analysis characterizing classical science. Such an approach, leading to what was called "the science of complexity", would aim to provide simple and relevant, though in principle incomplete, models of complex phenomena. It would emerge out of a synthesis of concepts developed around systems theory, cybernetics, self-organization models and the cognitive sciences.
We then examined a possible way to unify these concept by an in-depth analysis of complexity as an entanglement of on the one hand distinction, differentiation, variety, change, disorder, and on the other hand connection, integration, selection, invariance and order. It was shown that in order to have complexity, or even structure at all, both components, ordered and disordered, are necessary. The emergence and evolution of complex structures could then be understood as an interaction between these two components. The general process may be described as variation through recombination and mutation of (relatively stable) component systems, combined with the selective retention of invariant assemblies, thus forming higher-order stable systems. In contrast with biological variation-and-selection theories, however, we wanted to understand selective stabilization by the intrinsic organization of the assembly to be selected, not by the effect of an outside environment.
In order to model such internal stability we introduced a generalized concept of "closure". This may be understood by seeing an assembly as a collection of coupled subsystems, represented mathematically by relations or transformations. The assembly would then be closed if the coupling were such that some distinction, defining the identity of the system, would be invariant under the (sequential and parallel) application of the internal transformations. Four elementary types of closure were defined mathematically : transitive, cyclic, surjective and inverse surjective closure.
It was then hypothesized that all stable structures emerging through self-organization could be characterized by a specific combination of such elementary closures. Although this proposition could not be proven in the present stage of the research, it was lent some credibility by examining several examples of typical patterns of self-organization in which "closed" structures could be recognized.
It was also proposed that cognition is a process of internal self-organization whose function is to allow an actor to adapt to a complex environment by choosing appropriate action complexes. This process too can be analysed with the aid of the closure concept. However, the parallellism of internal, cognitive and external, physical self-organization is much more complex than it would appear to the naive observer, since there is in general no simple correspondence between internal and external distinctions. Cognitive distinctions are internally constructed with the aim of reducing subjective problem complexity, not with the aim of providing an objective picture of "reality".
This last assertion already points to the possibility of application of the emerging science of complexity. Indeed, a general theory of the dynamics and stabilization of distinctions based on the closure concept could help us to to solve our own complex problems. Practically such an application could be implemented as a computer-based support system (cfr. de Zeeuw, 1985), which would help actors to structure their problems, ideas and information, by recombination and closure of simple components. One example of an already functioning (and successful) medium for problem solving, based on algorithms for the variation and selection of simple rules (yet without explicit closure), is formed by "classifier systems" (Holland et al., 1986). Other existing computer supports are characterized by the fact that it is the user who introduces the variation, although the system helps him with the recombination and conceptual closure of his ideas. Examples of this type are : outliners (e.g. MORE or ThinkTank), hypermedia, conversational systems (Pask and Gregory, 1986), and a system like DEDUC (Bossel et al., 1982).
One of the challenges of a general theory of complexity based on the closure concept would then consist in the design of a a support system which would be more universal and more efficient than these existing applications.
Bibliography
Banathy B. (1984) : Systems Inquiry and the Science of Complexity : conceptual bases, in: New Principles and Technologies of Management, Banathy B. (ed.), (International Systems Institute , San Francisco).
Bossel H., Hornung B.R. & Müller-Reismann K-F. (1982)) : Kognitive Systemanalyse, (Institut für angewandte Systemforschung und Prognose, Hannover).
de Zeeuw G. (1985) : Problems of Increasing Competence, Systems Research 2, p. 13.
Dörner D. & Reither F. (1978) : 'Über das Problemlösen in sehr komplexen Realitätsbereichen', Zeitschrift für Experimentelle und Angewandte Psychologie 25.
Dörner D. (1983) : Heuristics and Cognition in Complex Systems, in: Methods of Heuristics, Groner R., Groner M. & Bischof W.F. (ed.), (Erlbaum, Hillsdale NJ), p. 89-107.
Heylighen F. (1987): Representation and Change. An Integrative Meta-representational Framework for the Foundations of Physical and Cognitive Science, (Ph. D. Thesis, Vrije Universiteit Brussel, Brussels).
Heylighen F. (1988) : Autonomy and Cognition as the Maintenance and Processing of Distinctions, in: Rosseel, Heylighen & Demeyere.
Heylighen F. (1988) : Formulating the Problem of Problem-Formulation, in: Cybernetics and Systems Research '88, Trappl R. (ed.), (Kluwer, Dordrecht), p. 949-957.
Holland J.H., Holyoak K.J., Nisbett R.E. & Thagard P.R. (1986): Induction: processes of inference, learning and discovery, (MIT Press, Cambridge MA).
Kauffman S.A. (1984): Emergent Properties in Random Complex Automata, Physica D 10, p. 145.
Mandelbrot B. (1982) : The Fractal Geometry of Nature, (Freeman, San Francisco).
Maturana H. and Varela F. (1980) : Autopoiesis and Cognition : the realization of the living, (Reidel, Dordrecht).
Mesarovic M.D. and Takahara Y. (1975) : General Systems Theory : Mathematical Foundations, (Academic Press, New York).
Mesjasz C. (1988) : Simplifying approaches to systems complexity - an idea of loopholes, in: Cybernetics and Systems '88, Trappl R. (ed.), (Kluwer Academic Publishers, Dordrecht), p. 69-76.
Nicolis G. & Prigogine I. (1986) : Exploring Complexity, (Piper Verlag ).
Pask G. & Gregory D. (1986): Conversational Systems, in: Human Productivity Enhancement (vol. II), Zeidner R. J. (ed.), (Praeger, ), p. 204-235.
Prigogine I. (1979) : From Being to Becoming : Time and Complexity in the Natural Sciences, ( Freeman, San Francisco).
Rosseel E., Heylighen F. & Demeyere F. (eds.) (1989) : Self-Steering and Cognition in Complex Systems. Toward a New Cybernetics, (in press) (Gordon and Breach, London).
Simon H.A. (1962): The Architecture of Complexity, Proceedings of the American Philosophical Society 106, p. 467-482, reprinted in :
Simon H.A. (1981) : The Sciences of the Articial (2nd ed.), (MIT Press, Cambridge MA).
Stadler M. & Kruse (1989) : Gestalt Psychology and the Theory of Self-Organization, in: Rosseel, Heylighen & Demeyere (1989).
Varela F.J. (1979) : Principles of Biological Autonomy, (North Holland, New York).
Vullierme J.L. (1987): Cybernétique auto-organisation cognition. La marche des sciences de la complexité, Revue Internationale de Systémique 1, p. 123.