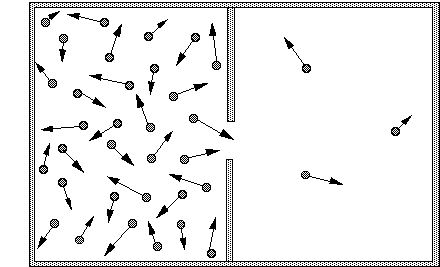
 Fig. : a box containing air molecules, divided in two compartments with a hole in the dividing wall. The arrows represent the direction and speed of movement of the molecules. Since there are many more molecules in the left compartment, there will also be many more molecules crossing the divide from left to right.
Fig. : a box containing air molecules, divided in two compartments with a hole in the dividing wall. The arrows represent the direction and speed of movement of the molecules. Since there are many more molecules in the left compartment, there will also be many more molecules crossing the divide from left to right.
The second law of thermodynamics states that in an isolated system the entropy will increase. In the statistical definition of entropy according to Boltzmann, this means that the system will evolve to its most probable state, that is, the one with the most homogeneous probability distribution. Let us explain this idea with a classical example: a closed box with two compartments (Fig. 1). The left compartment contains air, the right one is empty. Suppose that we make a hole in the wall separating the two compartments. An intuitive description of what happens is that air will be "sucked" out of the full compartment into the vacuum of the empty one, until both compartments contain equal amounts of air.
This effect is easy to understand when you look at the individual air molecules in the two compartments. The molecules are continuously flying in all directions, colliding with each other and with the walls of the compartment. A molecule bumping against the central wall separating the full compartment from the empty one will be reflected, and move back towards the middle of the full one. However, if the molecule would land on the hole, rather than on the separating wall, it would not be reflected but continue its journey rightwards into the empty compartment. Since many molecules are thus continuously flying from the left to the right, the number of molecules in the right compartment will quickly increase. These molecules too will collide and be scattered in all directions. Some of them will move to the left, into the hole, and thus go back to the left compartment. However, as long as there are less molecules in the right compartment, there will also be less that move through the hole from the right, and thus rejoin their erstwhile companions. As long as the concentration of molecules on the left is larger, there will be more movement from left to right than from right to left. Only when the concentration of molecules in the two compartments is uniform will there be an equal flow through the hole in both directions. This configuration where the distribution is homogeneous is the one with maximum entropy.
Now, it is in principle possible that by some coincidence more molecules would move to the left than to the right. This creates a difference in concentration between the two boxes, and therefore a decrease in entropy. However, since the amount of molecules in either compartment is so astronomically large, a very large number of them must move "countercurrent" to produce a noticeable difference. The probability that such a vast number of molecules would all move together in the same direction is vanishingly small. It is so small, in fact, that we can assume that it will never happen. Because of the law of large numbers, the larger the number of coincidences needed for an effect to occur, the smaller the probability that the effect will occur. And with numbers as large as the number of molecules in a gas, the resulting probability is as close to zero as you can practically get. Therefore, although entropy could decrease spontaneously, that is so improbable that the non-decrease of entropy has gotten the status of a law of thermodynamics. While we cannot predict the movement of the microscopic particles, the evolution towards homogeneity on the macroscopic scale is perfectly predictable.
Generalization
The reasoning we made about molecules diffusing to evenly fill a box can be easily generalized to the homogeneous diffusion of heat. Just replace molecules moving to another region by molecules transmitting their energy to another region. In all cases the mechanism underlying the growth of entropy is the same: if particles move in different directions with the same probability, they will evenly spread over all directions, and erase any differences in local density.
This formulation of the second law highlights the paradox underlying statistical mechanics. The equal probability of movement follows from classical mechanics, where all directions are considered equivalent. A particle might move backwards or forwards: there is no preference. Therefore, the average number of particles moving in a particular direction will depend only on the number of particles present, not on the direction. On average, more particles will move out of a high density region than out of a low density one. Therefore, high density regions will become relatively less dense, and the differences in density will disappear. On the microscopic level of the particle, all directions of change have the same probability. On the macroscopic level of the gas, however, one direction of change-towards greater homogeneity--has a much larger probability.
This preferred direction creates an "arrow of time". While classical mechanics does not really distinguish between past and future, statistical mechanics does. Time always flows in the direction of entropy increase, of greater homogeneity. This is progress of a kind, pushing evolution forward without ever allowing it to go back. But entropy increase is not what we usually call improvement. It is rather associated with the dissipation of energy, with wear and tear, with things running down and getting disorganized. Thus, thermodynamics has introduced irreversible change into the scientific world view. Yet, it still fails to explain the development of new organization which we normally associate with evolution.

